Description of an analysis page

The analysis pages are automatically generated at the end of a simulation and contain some information about the learned units. In this page we give a detailed explanation of them.

Optimal stimuli

S+
The optimal excitatory stimulus (S+) is the stimulus with norm 'r' that maximally excites the considered unit. 'r' is chosen to be the mean norm of the input stimuli, because we want S+ to be representative of the typical input. Since in the simulations described in the paper the units have a spatio-temporal receptive field, S+ has a component at time t (left) and one ad time t+dt (right). A comparison between the two patches hints at the time behavior of the unit. In this example, the unit responds best to a static oriented edge.
S-
The optimal inhibitory stimulus (S-) is the stimulus with norm 'r' that maximally inhibits the considered unit. In this example, the unit responds "worst" to a static edge orthogonal to S+.

Optimal parameters of S+

Optimal orientation: 0 deg at time t; 0 deg at time t+dt
Optimal frequency: 5.625 cycles/deg at time t; 5.625 cycles/deg at time t+dt
Optimal speed (phase change): -5 deg

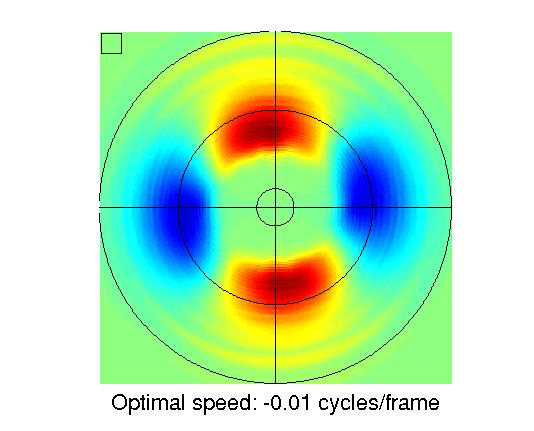
Using a two-dimensional Fourier analysis we extract from S+ several parameters that are used for example to generate the hexagonal test image (see below) or to make additional experiments with linear sine gratings. Here we report the orientation and frequency of the two components of S+ and the optimal speed, measured by the phase difference between S+ at time t and at time t+dt. The orientation is measured counterclockwise between 0 and 180 degrees, 0 being the horizontal direction. The frequency is reported in cycles/arc deg, assuming that an input patch is 0.5 arc deg large.

Response images

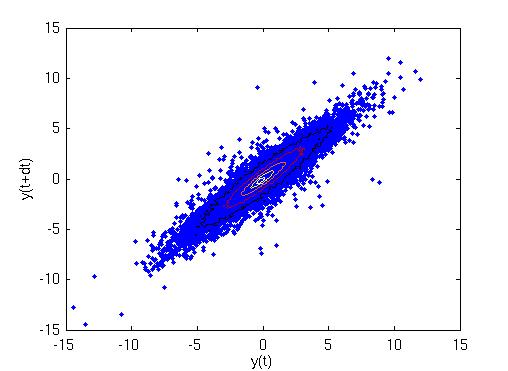
To study the response of the unit to a wide range of stimuli we use pairs of test images (one at time t and one at time t+dt). The response images are generated by scanning the test images, cutting at each point a 16x16 window, using it as an input to the unit, and plotting its output at the corresponding point. The black square in the upper left corner indicates the size of an input window.

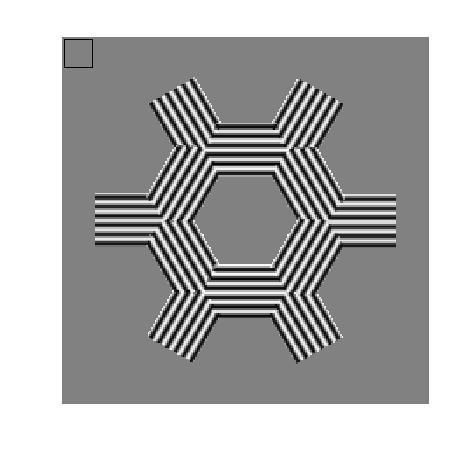
In the analysis pages we show two different types of response images. They are generated using the test images shown above (second row). The left one consists of a circular pattern of sine waves with frequencies increasing from the circumference to the center. The ring patterns move outward with the preferred speed of the unit. This test image gives information not only about the whole range of frequencies and orientations to which the unit responds or by which it is inhibited, but also about the sensitivity to phase. If a unit is sensitive, the response image will show oscillations in the radial direction, while if there are no oscillations the unit is phase-invariant. Moreover, since at two opposite points of a ring the grating is moving in opposite directions, different responses indicate selectivity to the direction of motion. The right test image is used to investigate end- and width-inhibition. The hexagonal shape is oriented such that it is aligned with the preferred orientation of the considered unit. The gratings are tuned to the preferred frequency and move at the preferred speed of the unit. If a unit is selective for the length or width of the input, one notices a higher response at the borders of the hexagon, where only part of the input window is filled, than in the inner, where the whole input window is filled.

Output statistics

In this section of an analysis page we study the response of the considered unit to a set of ca. 400,000 previously unseen frames and report some statistics.

Beta value: 0.058
The beta value is the quantity optimized by SFA, and measures the temporal variation of the output. It is here defined as
beta(y) = 1/(2*Pi) * sqrt(<dy/dt ^2>) .
In particular, a sine wave with period T has an beta value of 1/T.

Kurtosis: 19.74
Kurtosis is the fourth moment of the distribution of the output values. It is a measure of the sparseness of the unit, which is considered to be a desirable property of a neural code according to some efficiency arguments. We report it here to allow the comparison with other theoretical models of V1 [1].

Sparseness: 67 %
This is another measure of the sparseness of the unit. It is defined as
Sparseness(y) = (1- (<abs(y)>^2/<y^2>)) / (1-(1/n))
This measure is normalized such that 100% correspond to a unit responding to only one particular stimulus, while a unit scoring 0% responds to all stimuli. We report it here to allow the comparison with experimental studies [2].

The left graph shows the distribution of the output of the considered unit. The right graph shows a scatter plot of y(t) vs. y(t+dt) and gives a qualitative idea of the stability of the output of the units. Values lying along the diagonal y(t)=y(t+dt) are optimally stable in time. The superimposed lines are the contours of the joint distribution of y(t) and y(t+dt). The distances between the contours follow a logarithmic scale.

[1] B. Willmore and D.J.Tolhurst. (2001). Characterizing the sparseness of neural codes. Network: Comput. Neural Syst. 12, 255-270
[2] W.E. Vinje and J.L. Gallant. (2000). Sparse coding and decorrelation in primary visual cortex during natural vision. Science, 287, 1273-1276