sfa-tk : Slow Feature Analysis Toolkit for Matlab

Introduction

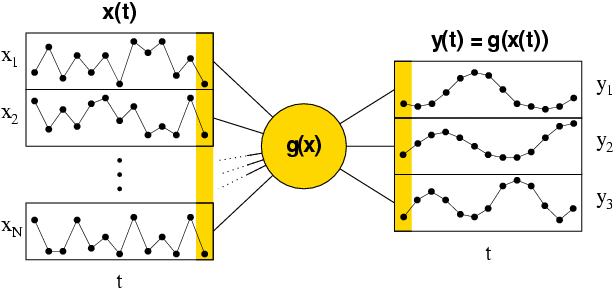
The Slow Feature Analysis Toolkit for Matlab sfa-tk v.1.0.1 is a set of Matlab functions to perform slow feature analysis (SFA). sfa-tk has been designed especially for experiments involving long and relatively high dimensional data sets.

SFA is an unsupervised algorithm that learns (nonlinear) functions that extract slowly-varying signals from their input data. The learned functions tend to be invariant to frequent transformations of the input and the extracted slowly-varying signals can be interpreted as generative sources of the observed input data. These properties make SFA suitable for many data processing applications and as a model for sensory processing in the brain. SFA is a one-shot algorithm, and it is guaranteed to find the optimal solution (within the considered function space) in a single step. For a detailed description see Wiskott, L. and Sejnowski, T.J. (2002). Slow Feature Analysis: Unsupervised Learning of Invariances. Neural Computation, 14(4):715-770. or refer to this online introduction by Laurenz Wiskott.

sfa-tk has been written by Pietro Berkes.

Download and Installation

Download sfa-tk v.1.0.1:
.tar.gz (ca. 8 kb): sfa_tk101.tar.gz

To install it, simply unpack the file into your favorite Matlab directory. This is going to create a sfa_tk directory. The two subdirectories sfa_tk/lcov and sfa_tk/sfa have to be added to the Matlab path variable MATLABPATH. The subdirectory sfa_tk/demo contains some demo functions, which you might want to run to make sure that everything is installed in the right way.

Changes from v.1.0beta:

Contact

sfa-tk has been tested in a variety of situations and I used it to perform some of my simulations. However, I had to make some changes in order to make it available online, mostly for esthetical reasons, and this might have introduced some bugs. Moreover, there are features which I rarely used (e.g. I hardly ever performed linear SFA). Finally, I'm sure that the endless imagination of the end-users is going to discover some untested, buggy corners of the toolkit.

If you find a bug or have any kind of feedback please contact me at p.berkes _AT_ biologie.hu-berlin.de.

Documentation




How to use sfa-tk

Level 1: I just need to put my data in and get the slow signals out

That's easy! Put your data in an array x, each variable on a different column and each data point on a different row (i.e. x(t,i) is the value of the i-th variable at time t). Then write

y = sfa1(x);
for linear SFA
or
y = sfa2(x);
for expanded (nonlinear) SFA.

The y array will contain the output signals produced by the functions learned by SFA, organized column by column just like the input signals and ordered by decreasing slowness, i.e. y(:,1) is the output signal of the slowest varying function, y(:,2) the output of the next slowest varying function, and so on up to y(:,size(y,2)), which corresponds to the output of the fastest varying function.

The default function space for expanded SFA is the space of polynoms of degree 2. To change it, refer to Level 3.

If you specify a second output argument with [y,hdl] = sfa1(x); or [y,hdl] = sfa2(x); you will get a reference to the SFA object containing the slowly varying functions themselves, which might be useful for example to apply them on test data: 


   % execute SFA on X_TRAIN
   [y_train, hdl] = sfa2(x_train);
   % apply the functions learned by SFA to the test data X_TEST
   y_test = sfa_execute(hdl, x_test);
   % clear the SFA object referred by the handle HDL
   sfa_clear(hdl);

This is probably the simplest way to use sfa-tk, but it limits the maximum size of your data set. The maximum number of input dimensions you can have in the linear case is more or less 5000 while in the quadratic case it is 100 (on a computer with 1.0 Gb RAM). The number of data points is also limited by the amount of memory of your system. To overcome these problems, you have to go up to Level 2.

Level 2: I have a large data set and need to have more control on the algorithm

The toolkit is designed such that the SFA algorithm can be divided in different steps: initialization, preprocessing, expansion and sfa. The single steps can be called more than once to update them, for example in the case your data set is too long or if you need to generate input data on-the-fly. A typical sfa-tk script has this structure (for a detailed description of the single functions and their options refer to the Matlab help or to the online documentation): 


   % create an SFA object and get a reference to it
   hdl = sfa2_create(pp_dim, sfa_range, 'PCA');

   % loop over your data
   while data_available(),
      % load or generate the next data set
      x = get_data();
      % update the preprocessing step
      sfa_step(hdl, x, 'preprocessing');
   end

   % loop over your data
   while data_available(),
      % load or generate the next data set
      x = get_data();
      % update the expansion step
      sfa_step(hdl, x, 'expansion');
   end

   % close the algorithm
   sfa_step(hdl, [], 'sfa');

   % save the results
   sfa_save(hdl, 'filename');

   % ... do something with your data ...

   % clear the SFA object referred by the handle HDL
   sfa_clear(hdl);

Of course you can do better than this: 


   % create an SFA object and get a reference to it
   hdl = sfa2_create(pp_dim, sfa_range, 'PCA');

   % loop over the two SFA steps
   for step_name = {'preprocessing', 'expansion'},

      % loop over your data
      while data_available(),
         % load or generate the next data set
         x = get_data();
         % update the current step
         sfa_step(hdl, x, step_name{1});
      end

   end
   % close the algorithm
   sfa_step(hdl, [], 'sfa');

   % save the results
   sfa_save(hdl, 'filename');

   % ... do something with your data ...

   % clear the SFA object referred by the handle HDL
   sfa_clear(hdl);

Level 3: I want to perform expanded SFA and define my own function space

In its general (nonlinear) formulation, SFA has to expand the input data using a basis of the function space you want to use. In sfa-tk this is done by the function expansion. The default function implements an expansion in the space of all polynoms of degree two (which explains the prefix sfa2 before some of the functions). If you want to implement your own function space, you have to overwrite the function expansion and the function xp_dim, which returns the dimension of the expanded space given the number of input variables.

Example

Assume you want to find the slowest varying functions in the space formed by all linear combinations of the signals and of the signal to the fourth. If the input space has dimension N, the expanded space will have dimension 2*N.

The expansion function is going to look like this: 


   function x = expansion(hdl, x),
      x = cat(2, x, x.^4);
The first argument (hdl) is ignored in this case. It might be useful if you want the expanded space to be controlled by some parameters. E.g. if you want it to be spanned by random radial basis functions, you can generate random mean vectors and variances and add them to the structure SFA_STRUCTS{hdl} (see below), and then use them in your expansion function.

You also need to overwrite the xp_dim function: 


   function dim = xp_dim( input_dim ),
      dim = 2*input_dim;

Make sure that the new functions are in the current directory or appear in your path list before the default versions!

Structure of an SFA object

The SFA objects are stored in the global cell array SFA_STRUCTS. Their handle is equal to their index in this array. The SFA objects are structures with following fields:

You can of course insert additional fields to this structure if necessary (for example to add some data that has to be used by the expansion function, see above).

Brief description of the demo scripts

In the directory sfa_tk/demo you can find four demo scripts:

How to cite sfa-tk

If you use sfa-tk for scientific reasons you might need to cite it. Here is the official way to do it:

P.Berkes (2003)
sfa-tk: Slow Feature Analysis Toolkit for Matlab (v.1.0.1).
http://itb.biologie.hu-berlin.de/~berkes/software/sfa-tk/sfa-tk.shtml